Phffff=blog===
Guide
-
Programming Languages
- Find Functions by Type in Python
- A Look at Swift
- Converting a Codebase to mypy
- Example of Type-Based Optimizations in Factor
- A Short Guide to Adding a Keyword to Go
- A Short Guide to Creating Babel Plugins
-
Misc.
-
Distributed Systems
-
Reads
-
Approximate Computing
- Exploring Loop Perforation Opportunities in OCaml Programs
- The Difficulty in a General Approximate Computing Framework
-
Pages
📎 Find Functions by Type in Python
10 Jan 2020
After adding types to my project, I became curious if there was a way to programmatically query my project’s functions based on type. The inspect module has a signature function that returns the annotated type signature, which makes this possible.
In this example I will query from the User module of my learn project.
First, I create a list of function names and their signature.
res = []
for f in dir(User):
x = getattr(User, f)
if not callable(x):
continue
try:
res.append((f, inspect.signature(x)))
except:
continue
The value of res looks like this
[...
('get_setting_value', <Signature (self, name: str) -> Union[str, NoneType]>),
('is_teacher', <Signature (self) -> bool>),
('is_teacher_of_survey', <Signature (self, survey: 'Survey') -> bool>),
('open_surveys', <Signature (self, now: datetime.datetime) -> List[ForwardRef('Survey')]>),
('set_password', <Signature (self, password: str) -> None>),
('set_setting', <Signature (self, name: str, value: str) -> None>),
('started_survey', <Signature (self, *, survey: 'Survey') -> bool>),
('stylize_for_import', <Signature (user: List[str]) -> List[str]>),
('wants_easy_input', <Signature (self) -> bool>),
...]
I can now make a function that, for example, finds all functions that could return a specific type. By “could return” I mean that the type could be wrapped in a list, union, or forwardref. There are other possibilities, like sets and dicts, but I didn’t get that far.
def could_return(t):
ret = []
for name, sig in res:
if type_in(t, sig.return_annotation):
ret.append((name, sig))
return ret
This requires a type_in helper function, which we can define
by going over a few cases that I’m interested in.
def type_in(t, tt):
if t == tt:
return True
if hasattr(tt, '__origin__'):
if tt.__origin__ == list:
assert len(tt.__args__) == 1
return type_in(t, tt.__args__[0])
if tt.__origin__ == typing.Union:
return any([type_in(t, ttt) for ttt in tt.__args__])
if tt.__class__ == typing.ForwardRef:
return type_in(t, tt.__forward_arg__)
return False
The code is a little awkward since there is no clean type inspection API that I know of.
Now, we can query
>>> could_return(bool)
[...
('is_teacher', <Signature (self) -> bool>),
('is_teacher_of_survey', <Signature (self, survey: 'Survey') -> bool>),
('started_survey', <Signature (self, *, survey: 'Survey') -> bool>),
('wants_easy_input', <Signature (self) -> bool>),
...]
>>> could_return('Survey')
[...
('accessible_surveys', <Signature (self) -> List[ForwardRef('Survey')]>),
...]
>>> could_return(str)
[...
('get_setting_value', <Signature (self, name: str) -> Union[str, NoneType]>),
('stylize_for_import', <Signature (user: List[str]) -> List[str]>),
...]
📎 A Look at Swift
09 Dec 2019
I’ve been meaning to look at Swift, and I think Advent of Code is a good excuse.
$ docker run --rm -it swift
root@c3358942d62e:/# swift
error: failed to launch REPL process: process launch failed: 'A' packet returned an error: 8
Awkward.
https://github.com/apple/swift-docker/issues/9
$ docker run --privileged --rm -it swift
root@d8fe53a62296:/# swift
Welcome to Swift version 5.1 (swift-5.1.2-RELEASE).
Type :help for assistance.
1> print("hi")
hi
2>
I’ll try to solve the first question with Swift.
import Foundation
func proc(x: Int) -> Int {
return x / 3 - 2
}
let lines = try String(contentsOfFile: "1.txt").split{ $0.isNewline }
var agg = 0
for line in lines {
agg += proc(x: Int(String(line))!)
}
print(agg)
This works. Being a relatively new language, I thought there might be support for map, fold, and anonymous funtions. I was right:
import Foundation
func proc(x: Int) -> Int {
return x / 3 - 2
}
let lines = try String(contentsOfFile: "1.txt").split{ $0.isNewline }
print(lines.map({proc(x: Int(String($0))!)}).reduce(0, +))
I now tried to solve part 2.
import Foundation
func proc(x: Int) -> Int {
let res = x / 3 - 2
if res > 0 {
return res + proc(x: res)
}
return 0
}
let lines = try String(contentsOfFile: "1.txt").split{ $0.isNewline }
print(lines.map({proc(x: Int(String($0))!)}).reduce(0, +))
Using swift was hard at first (solving the docker issue) but it reads pretty nicely in this very simple use. I’m not sure what to think about the tagged arguments though.
📎 Converting a Codebase to mypy
31 Oct 2019
mypy is a static type checker for Python. I’ve tried twice before to use it on an existing codebase but was always turned off by all of the initial import errors. I’ve tried again and have succeeded in getting past the initial pain. In this post I will document my journey.
The project I’m adding mypy to is called ‘learn’. It is a webapp using flask. It has 3.5k lines of Python; so not too large.
$ mypy learn
learn/strings.py:7: error: Cannot find module named 'flask_babel'
learn/__init__.py:13: error: Cannot find module named 'flask_sqlalchemy'
learn/__init__.py:13: note: See https://mypy.readthedocs.io/en/latest/running_mypy.html#missing-imports
learn/__init__.py:14: error: Cannot find module named 'flask_login'
learn/__init__.py:15: error: Cannot find module named 'flask_babel'
learn/logs.py:13: error: Cannot find module named 'flask_login'
learn/logs.py:17: error: Item "None" of "Optional[Any]" has no attribute "before_request"
learn/logs.py:28: error: Item "None" of "Optional[Any]" has no attribute "teardown_request"
learn/errors.py:9: error: Item "None" of "Optional[Any]" has no attribute "errorhandler"
learn/errors.py:14: error: Item "None" of "Optional[Any]" has no attribute "errorhandler"
learn/models/user.py:7: error: Cannot find module named 'flask_login'
learn/models/user.py:12: error: Name 'db.Model' is not defined
learn/models/user.py:15: error: Item "None" of "Optional[Any]" has no attribute "Column"
learn/models/user.py:15: error: Item "None" of "Optional[Any]" has no attribute "Integer"
learn/models/user.py:16: error: Item "None" of "Optional[Any]" has no attribute "Column"
[many more lines]
Found 371 errors in 15 files (checked 17 source files)
Lots of errors.
I remembered that some libraries probably don’t have
stub files.
So I created stubs for flask_babel, flask_sqlalchemy, and flask_login.
$ touch stubs/flask_babel.pyi
$ touch stubs/flask_sqlalchemy.pyi
$ touch stubs/flask_login.pyi
$ MYPYPATH=./stubs mypy learn
Less errors now. I next chose one error and tried to fix it.
learn/routes/question.py:11: error: Module 'flask_login' has no attribute 'login_required'
The line it points to is
from flask_login import login_required
So it seems I first need to add stuff to the stubs. Specifically, everything I import from any library without its own types I’ll have to add to the stub file and give it a type (I could just give it the type Any, but that won’t do much good)
So,
login_required is a decorator.
I found some info in a mypy issue
on typing decorators.
Since login_required won’t change the type of the function it decorates,
I choose to type it as follows:
from typing import TypeVar, Callable
T = TypeVar('T')
def login_required(f: T) -> T: ...
I’ll now choose a different error.
learn/routes/survey.py:10: error: Module 'flask_login' has no attribute 'current_user'
I want to give this the type learn/models/user/User from my own code.
To do this I imported the class in the stub file.
from learn.models import User
From there I kept adding types to my code.
I quickly realized that the body of function won’t be typechecked
unless the function itself is given a type.
This can be changed by using the --strict flag for mypy.
However that becomes a little too strict initially.
Currently I’m going through the codebase enabling, one at a time,
the flags which --strict enables. I’ve found if I enable them all at once
then there’s too many errors to focus on.
Practically, I haven’t found any huge bugs yet,
but mypy has caught a few instances where, in a list comprehension,
I do operations without checking for None
when dealing with Optional[Blah].
The big win so far is with documentation. There are a lot of functions that I have forgotten exactly what they return. Using mypy has forced me to figure it out and then add the type, which is a form of checkable documentation.
It’s also improved my code. For example, there were times which I would reassign a variable to some modified version of itself, taking on a new type. This code is hard to maintain. So when mypy shows me exactly where I’m doing this I have an opportunity to refactor it.
📎 Applying Reflective Consistency to Software Transactional Memory
22 Jul 2019
This post will describe adding reflective consistency to a software transactional memory (STM) implementation in go.
The github.com/lukechampine/stm package implements STM for go. The important function is verify, which checks that all of the read STM variables in the current transaction still hold the same values (it does this by tracking and comparing a version number). This logic is triggered inside Atomically, the ‘runner’ for atomic transactions. Adding reflective consistency to Atomically is simple:
@@ -189,6 +190,11 @@ func catchRetry(fn func(*Tx), tx *Tx) (retry bool) {
return
}
+var commit_attempts = 0
+var anomalies = 0
+var target_anomaly_rate = 0.05
+
// Atomically executes the atomic function fn.
func Atomically(fn func(*Tx)) {
retry:
@@ -204,9 +210,18 @@ retry:
}
// verify the read log
globalLock.Lock()
+ commit_attempts += 1
if !tx.verify() {
- globalLock.Unlock()
- goto retry
+ anomaly_rate := float64(anomalies) / float64(commit_attempts)
+ if anomaly_rate >= target_anomaly_rate {
+ globalLock.Unlock()
+ goto retry
+ } else {
+ anomalies += 1
+ }
Now, 5% of transactions which should not be allowed (due to stale versions) are allowed to commit.
I have not found any great application for this code yet. An ideal application would have expensive retries (meaning allowing 5% through will speed things up) and not too high cost of stale data (meaning 5% anomalies don’t cause too much trouble for the program or its users).
📎 First Free Workspace in i3
16 Jul 2019
i3 is an excellent tiling window manager. Soon after I started using it I wanted a way to switch to the first unused workspace. I didn’t see any built in way to do this, but I knew that i3 had python bindings. The following script switches to the first unused workspace (only considering the default ones numbered 1 to 10):
#!/usr/bin/env python
"""
Find the first free workspace and switch to it
Add this to your i3 config file:
bindsym <key-combo> exec python /path/to/this/script.py
"""
import i3
def main():
workspaces = i3.get_workspaces()
workints = list()
for w in workspaces:
workints.append(w['name'])
for i in range(1,11):
if str(i) not in workints:
i3.workspace(str(i))
break
if __name__ == '__main__':
main()
As the documentation for the script suggests, I have the following in my i3 config file to bind the script to win+~:
bindcode $mod+49 exec python ~/.i3/firstfree.py
📎 Checking, but not enforcing, Transaction Semantics
28 Jun 2019
Checking against transaction semantics is much easier than enforcing transaction semantics.
One way to check is to track versions for every value, for every replica. A derivation of version vectors can be used.
We’ll assume key-value API of get and put over single keys.
The get will return, in addition to the value, its version.
A put will contain, in addition to the updated value, the name and versions of
all of its dependent keys.
For example, the operation y = x + y where x and y are backed
by the key-value store would look like the following:
x, version_x = get('x')
y, version_y = get('y')
put('y', x + y, {'x': version_x, 'y': version_y})
The server can then check the versions of the keys to see if stale values were used.
What does this buy us? This can be used to implement reflective consistency.
📎 Reads in Raft
26 Jun 2019
Writes are inserted into the raft log; there is a total order of writes. But what about reads?
Let’s look at Consul. Consul offers three consistency levels:
- consistent: leaders respond to reads but first confirm their leader status; and
- default: leaders respond to reads but do not confirm their status as leader;
- stale: followers can respond to reads.
In all cases, reads are not inserted into the log. Several problem can arise.
Problem 1: there could be uncommitted writes which were received before the read. These writes arrived before the read but haven’t made it through the raft protocol yet. This means we get stale reads. If reads went through the raft protocol we’d avoid this issue (this is a trade-off, the read would be correct but it’d be much slower). This applies to the consistent consistency level.
Problem 2: there could be committed writes that the current node doesn’t know about. Problem 2a: a node assumes it’s the leader, but it’s not, and services reads. This applies to the default consistency level. Problem 2b: the follower hasn’t learned about a write yet. This applies to the stale consistency level.
There are potential problems in each consistency level of Consul. I believe there is room for a reflective consistency solution for users that can accept some level of anomalies. They would then be able to describe their ideal anomaly rate and the system would then adapt its consistency level to accommodate.
📎 Reading 'Spectre is here to stay'
14 Mar 2019
Spectre is here to stay: An analysis of side-channels and speculative execution
This paper addresses three open problems made more relevant since Spectre:
- finding side-channels
- understanding speculative vulnerabilities
- mitigating them
This paper begins by introducing a formal model for CPU architectures in order to study spectre. They distinguish the observable state of an architecture (what a developer might see from its API) from the micro architecture (extra state kept by the CPU). They then study the model and a class of attacks known as side-channel attacks. Whenever state is exposed from the micro architecture, there is a possibility of an attacker to gain information they should not have. For example, speculative execution can cause data to be read into a cache. Based on timing, an attacker might gain some information about the, perhaps confidential, data.
A main result from their study is that in most programming languages
with timers, speculative vulnerabilities on most modern CPUs allow for
the construction of a (well-typed) function with signature
read(address: int, bit: int) → bit. Frightening.
The paper then describes possible mitigations and their runtime impact.
The authors experimented with mitigations in the V8 JavaScript engine.
For instance, one mitigation was to augment every branch with an LFENCE
instruction (as suggested by Intel). This led to a 2.8x slowdown on
the Octane JavaScript benchmark.
Another mitigation,
retpoline,
led to a 1.52x slowdown on Octane.
Unfortunately,
none of the mitigations completely protect against Spectre.
📎 Reading 'A Generalised Solution to Distributed Consensus'
21 Feb 2019
A Generalised Solution to Distributed Consensus
This paper generalizes Paxos and Fast Paxos into a model of write-once registers and provides three consensus algorithms for this model.
What caught my eye in this paper is this quote from the first page
This paper aims to improve performance by offering a generalised solution allowing engineers the flexibility to choose their own trade-offs according to the needs of their particular application and deployment environment.
This jibes with the goal of reflective consistency. Developers using reflective consistency can choose their own tradeoffs on the correctness/time curve. They can sacrifice the consistency of their system to improve its reactiveness.
Instead of the correctness/time curve, each of the alternative algorithms proposed in this paper fall somewhere on a curve balancing tradeoffs between Paxos and Fast Paxos.
Generalized Distributed Consensus
The authors reframe distributed consensus into the processing of write-once registers. They separate processes into servers, storing values, and clients, getting and putting values. They state that solving consensus means ensuring all of the following:
Non-triviality - All output values must have been the input value of a client.
Agreement - All clients that output a value must output the same value.
Progress - All clients must eventually output a value if the system is reliable and synchronous for a sufficient period.
Their general solution organizes write-once registers into the following taxonomy
- Quorums: non-empty sets of servers.
- Decided register values: when a quorum has identical, non-nil values for any register.
- Register sets: the sets containing a copy of a single register from each server.
They then go on to define a general algorithm to establish consensus. I could not keep up with the discussion of the algorithm, but it seemed well-grounded. In the end they offer proofs for their algorithms but passingly mention that one goal of this work is to create a general enough model for distributed consensus so that the correctness of its algorithms become obvious. Sounds tough to me, but what a noble goal!
Questions
Modern distributed consensus often means Raft. I’m curious if this could generalize raft in addition to Paxos and Fast Paxos.
It’d be interesting to see a benchmark comparing the different example consensus algorithms proposed in section 6.
📎 Reflective Consistency
14 Jan 2019
Reflective consistency is a consistency model which exposes anomaly statistics to the user. The anomalies are defined by some underlying consistency model. For example, a system could run under eventual consistency but track anomalies as defined by linearizability. Statistics on these anomalies can then be used by the system or the user of such a system. One example of using the statistics is for modifying the underlying consistency model.
Example: Cassandra with Reflective Consistency
Cassandra offers many consistency levels1 under which every read and write can be performed. A user could request Cassandra to perform all writes under a strong consistency level, such as requiring a quorum of replicas to acknowledge every write, and all reads under a relatively weaker consistency level.
Using the anomaly statistics, a user could modify their use of Cassandra based on anomalies. A user could perform all writes under the same, weak consistency level as reads, and when anomalies start to increase more than the user wants they could direct Cassandra to use the stronger consistency level until anomalies being to decrease.
Statistics could even be tracked per key, per replica, or per anything. This gives the user fine or coarse grained control.
📎 Example of Type-Based Optimizations in Factor
30 Jun 2018
Factor is dynamically typed, yet with words such as declare and TYPED: we can guide the compiler to generate more efficient code.
Consider the following two words and their definitions:
: add-untyped ( x y -- z ) + ;
TYPED: add-typed ( x: fixnum y: fixnum -- z: fixnum ) + ;
We will use the
disassemble
word for viewing assembly.
Let’s now compare the difference between add-untyped
and add-typed.
First, add-untyped:
00007f134c061820: 8905da27f4fe mov [rip-0x10bd826], eax
00007f134c061826: 8905d427f4fe mov [rip-0x10bd82c], eax
00007f134c06182c: 488d1d05000000 lea rbx, [rip+0x5]
00007f134c061833: e9e8f115ff jmp 0x7f134b1c0a20 (+)
Very simple, this jumps to the generic word +
which will dynamically dispatch to the appropriate + definition for fixnum.
And now add-typed:
00007f134c041c90: 89056a23f6fe mov [rip-0x109dc96], eax
00007f134c041c96: 53 push rbx
00007f134c041c97: 498b06 mov rax, [r14]
00007f134c041c9a: 4983ee08 sub r14, 0x8
00007f134c041c9e: 4983c708 add r15, 0x8
00007f134c041ca2: 498907 mov [r15], rax
00007f134c041ca5: e8d65dfefe call 0x7f134b027a80 ([ \ integer>fixnum-strict ~array~ 0 ~array~ inline-cache-miss ])
00007f134c041caa: 498b07 mov rax, [r15]
00007f134c041cad: 4983c608 add r14, 0x8
00007f134c041cb1: 4983ef08 sub r15, 0x8
00007f134c041cb5: 498906 mov [r14], rax
00007f134c041cb8: e8c35dfefe call 0x7f134b027a80 ([ \ integer>fixnum-strict ~array~ 0 ~array~ inline-cache-miss ])
00007f134c041cbd: 89053d23f6fe mov [rip-0x109dcc3], eax
00007f134c041cc3: 5b pop rbx
00007f134c041cc4: 488d1d05000000 lea rbx, [rip+0x5]
00007f134c041ccb: e950ffffff jmp 0x7f134c041c20 (( typed add-typed ))
This first tries to coerce the two inputs to fixnum and then jumps to an
address marked as (( typed add-typed )). The assembly for (( typed add-typed )) is
00007f134c041c20: 8905da23f6fe mov [rip-0x109dc26], eax
00007f134c041c26: 53 push rbx
00007f134c041c27: 498b06 mov rax, [r14]
00007f134c041c2a: 498b5ef8 mov rbx, [r14-0x8]
00007f134c041c2e: 4801c3 add rbx, rax
00007f134c041c31: 0f801a000000 jo 0x7f134c041c51 (( typed add-typed ) + 0x31)
00007f134c041c37: 4983ee08 sub r14, 0x8
00007f134c041c3b: 49891e mov [r14], rbx
00007f134c041c3e: 8905bc23f6fe mov [rip-0x109dc44], eax
00007f134c041c44: 5b pop rbx
00007f134c041c45: 488d1d05000000 lea rbx, [rip+0x5]
00007f134c041c4c: e96f5dfefe jmp 0x7f134b0279c0 ([ \ integer>fixnum-strict ~array~ 0 ~array~...)
00007f134c041c51: e80a1a45ff call 0x7f134b493660 (fixnum+overflow)
00007f134c041c56: 8905a423f6fe mov [rip-0x109dc5c], eax
00007f134c041c5c: 5b pop rbx
00007f134c041c5d: 488d1d05000000 lea rbx, [rip+0x5]
00007f134c041c64: e9575dfefe jmp 0x7f134b0279c0 ([ \ integer>fixnum-strict ~array~ 0 ~array~...)
This will do an add instruction directly and then check for overflow.
No dynamic dispatch involved.
Let’s test these out with some input values.
We’ll look at the assembly for [1 2 add-untyped] and then [1 2 add-typed].
First, using add-untyped:
00007f134c148370: 89058abce5fe mov [rip-0x11a4376], eax
00007f134c148376: 4983c610 add r14, 0x10
00007f134c14837a: 49c70620000000 mov qword [r14], 0x20
00007f134c148381: 49c746f810000000 mov qword [r14-0x8], 0x10
00007f134c148389: 890571bce5fe mov [rip-0x11a438f], eax
00007f134c14838f: 488d1d05000000 lea rbx, [rip+0x5]
00007f134c148396: e98594f1ff jmp 0x7f134c061820 (add-untyped)
00007f134c14839b: 0000 add [rax], al
00007f134c14839d: 0000 add [rax], al
00007f134c14839f: 00 invalid
As expected, this jumps to add-untyped.
And now using add-typed:
00007f134c146850: 8905aad7e5fe mov [rip-0x11a2856], eax
00007f134c146856: 4983c610 add r14, 0x10
00007f134c14685a: 49c70620000000 mov qword [r14], 0x20
00007f134c146861: 49c746f810000000 mov qword [r14-0x8], 0x10
00007f134c146869: 890591d7e5fe mov [rip-0x11a286f], eax
00007f134c14686f: 488d1d05000000 lea rbx, [rip+0x5]
00007f134c146876: e9a5b3efff jmp 0x7f134c041c20 (( typed add-typed ))
00007f134c14687b: 0000 add [rax], al
00007f134c14687d: 0000 add [rax], al
00007f134c14687f: 00 invalid
This directly jumps to (( typed add-typed )) which will directly do the add instruction.
The compiler safely skipped the type coercion as it knows the inputs are both fixnum.
📎 A Short Guide to Adding a Keyword to Go
13 Jan 2018
Go is a programming language.
Sometimes code looks cleaner when variable declarations are listed after code that uses them. Imagine writing Go in this style.
$ cat test.go
package main
import (
"fmt"
"strconv"
)
func main() {
fmt.Println("hi")
fmt.Println(f(a))
andwhere a = 1
andwhere f = func(a int) string { return strconv.Itoa(a+1) }
}
$ ./bin/go run test.go
hi
2
Below are the modifications I made to the Go compiler.
- The string “andwhere” is associated with a new token
_Andwhere:
--- a/src/cmd/compile/internal/syntax/tokens.go
+++ b/src/cmd/compile/internal/syntax/tokens.go
@@ -46,6 +46,7 @@ const (
_Continue
_Default
_Defer
+ _Andwhere
_Else
_Fallthrough
_For
@@ -118,6 +119,7 @@ var tokstrings = [...]string{
_Continue: "continue",
_Default: "default",
_Defer: "defer",
+ _Andwhere: "andwhere",
_Else: "else",
_Fallthrough: "fallthrough",
_For: "for",
- The new AST node
Andwhereholds a declaration statement:
--- a/src/cmd/compile/internal/syntax/nodes.go
+++ b/src/cmd/compile/internal/syntax/nodes.go
@@ -371,6 +371,11 @@ type (
stmt
}
+ Andwhere struct {
+ S *DeclStmt
+ stmt
+ }
+
ReturnStmt struct {
Results Expr // nil means no explicit return values
stmt[
Andwherestatements are parsed in the statement parsing functionstmtOrNil:
--- a/src/cmd/compile/internal/syntax/parser.go
+++ b/src/cmd/compile/internal/syntax/parser.go
@@ -2034,6 +2053,11 @@ func (p *parser) stmtOrNil() Stmt {
case _Go, _Defer:
return p.callStmt()
+ case _Andwhere:
+ s := new(Andwhere)
+ s.S = p.declStmt(p.varDecl)
+ return s
+
case _Goto:
s := new(BranchStmt)
s.pos = p.pos()
- Every
Andwhereis moved to the beginning of its surrounding function body at end of the function declaration parsing functionfuncDeclOrNil:
@@ -542,9 +543,27 @@ func (p *parser) funcDeclOrNil() *FuncDecl {
}
f.Pragma = p.pragma
+ // Lift all Andwhere to the top
+ if f.Body != nil {
+ f.Body.List = lift_andwheres(f.Body.List)
+ }
+
return f
}
+func lift_andwheres(list []Stmt) []Stmt {
+ for i, x := range list {
+ switch x.(type) {
+ case *Andwhere:
+ removed := append(list[:i], list[i+1:]...)
+ modified := x.(*Andwhere).S
+ prepended := append([]Stmt{modified}, removed...)
+ return lift_andwheres(prepended)
+ }
+ }
+ return list
+}
+
func (p *parser) funcBody() *BlockStmt {
p.fnest++
errcnt := p.errcnt
📎 A Short Guide to Creating Babel Plugins
12 Jan 2018
Babel is a JavaScript compiler with plugin support.
Imagine a Babel plugin
that transforms all string literals into
"babel".
The source below does that.
module.exports = function () {
return {
visitor: {
StringLiteral: function a(path) {
path.node.value = 'babel';
}
}
};
};
Here’s how to use it:
$ npm install babel babel-cli
$ ./node_modules/.bin/babel --plugins ./a.js
a = 'hi';
^D
a = 'babel';
It works with files too:
$ cat b.js
var s = 'start';
function go() {
var e = 'end';
return s + e;
}
console.log(go());
$ ./node_modules/.bin/babel --plugins ./a.js ./b.js
var s = 'babel';
function go() {
var e = 'babel';
return s + e;
}
console.log(go());
$ ./node_modules/.bin/babel --plugins ./a.js ./b.js | node
babelbabel
Now imagine the same babel plugin that, in addition, transforms every
variable declaration in a function initialized to '*' to be
abstracted as a function argument.
The source below does that.
module.exports = function (babel) {
t = babel.types
return {
visitor: {
StringLiteral: function a(path) {
path.node.value = 'babel';
},
VariableDeclaration: function a(path) {
var var_name = path.node.declarations[0].id.name;
var var_val = path.node.declarations[0].init.value;
if (var_val === '*') {
path.parentPath.parentPath.node.params.push(t.identifier(var_name));
path.node.declarations[0].init = t.identifier(var_name);
}
},
}
};
};
Here’s how to use it:
$ cat c.js
function go(t) {
var c = 'hi';
var a = '*';
for (var i = 0; i < t; ++i) {
console.log(c + ' ' + a);
}
}
go(5, 'stranger')
$ ./node_modules/.bin/babel --plugins ./a.js ./c.js | node
babelbabelbabel
babelbabelbabel
babelbabelbabel
babelbabelbabel
babelbabelbabel
$ ./node_modules/.bin/babel --plugins ./a.js ./c.js
function go(t, a) {
var c = 'babel';
var a = a;
for (var i = 0; i < t; ++i) {
console.log(c + 'babel' + a);
}
}
go(5, 'babel');
📎 Exploring Loop Perforation Opportunities in OCaml Programs
09 Aug 2016
Approximate computing is sacrificing accuracy in the hopes of reducing resource usage. Loop perforation is an approximate programming technique with a simple story: skip loop iterations whenever we can. This simple idea is why loop perforation is one of the simplest approximate programming techniques to understand and apply to existing programs. Computations often use loops to aggregate values or to repeat subcomputations until a convergence. Often, it is acceptable to simply skip some of the values in an aggregation or to stop a computation before it has a chance to converge.
This summer I’ve been working on a handful of projects at OCaml Labs in the pleasant city of Cambridge, UK. Part of my work has been in creating a tool for loop perforation.
Aperf
aperf
(opam,
github) is a
research quality
tool
for exploring loop perforation opportunities in OCaml programs.
Aperf takes a user-prepared source file,
instructions on how to build the program,
and a way to evaluate its accuracy,
and will try to find a good balance
between high speedup and low accuracy loss.
It does this by testing perforation configurations
one by one.
A perforation configuration is a perforation percentage for each
for loop which the user requests for testing.
A computation with four perforation hooks will have configurations
like [0.13; 1.0; 0.50; 0.75], etc.
Aperf searches for configurations to try either
by exhaustively enumerating all possibilities or by
pseudo-smartly using optimization techniques.
Aperf offers hooks into its system in the form of
ppx annotations
and Aperf module functions in a source file.
A user annotates for loops as
for i = 1 to 10 do
work ()
done [@perforate]
Upon request, aperf can store the amount of perforation into a reference variable:
let p = ref 1. in
for i = 1 to 10 do
work ()
done [@perforatenote p]
This could be useful for extrapolating an answer.
Right now, the only Aperf module function used for hooking
perforation is Aperf.array_iter_approx which has
the same type as Array.iter.
If this tool makes it out of the research stage then
we will add more perforation hooks.
(They are easy to add, thanks to
ppx_metaquot.)
Optimizing
Right now we only support exhaustive search and hill climbing. Better strategies, including interacting with nlopt and its ocaml bindings, could be a future direction.
Our hill climbing uses the fitness function described in Managing Performance vs. Accuracy Trade-offs with Loop Perforation1:
The b parameter (which we also call the accuracy loss bound) is for controlling the maximum acceptable accuracy loss as well as giving more weight to the accuracy part of the computation. In other words, a perforation solution must work harder at maintaining low accuracy loss than in speeding up the computation.
Limitations
OCaml programs don’t usually use loops.
This is what initially led us to offer Aperf.array_iter_approx
Programs must have a way to calculate the accuracy of perforated answers. This is a huge limitation in practice because usually this means the user of aperf must knowing the answer ahead of time. In a lot of domains this is unfeasible. Finding applicable domains is an ongoing problem in approximate computing.
Examples
Summation
Summing $m$ out of $n$ numbers sounds boring but it’s a good place to start. This problem is interesting because there are theoretical bounds to compare results to. Hoeffding’s Inequality tells us what we can expect for absolute error. The following graph gives maximum absolute error, with confidence of 95%, when keeping and summing $m$ variables out of 100 where each variable is drawn uniformly from the range $[0,100{,}000]$.
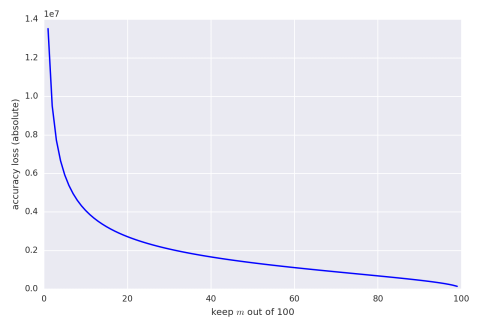
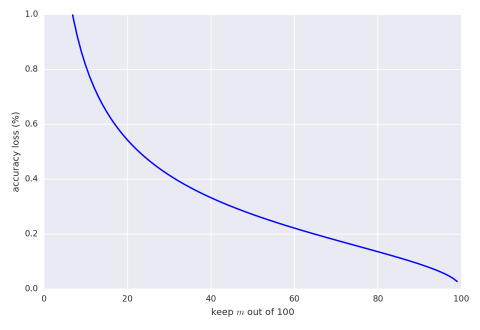
We can also give the same graph with percentage bounds (assuming the result is 5,000,000).
Our code for summing is a little awkward because aperf cannot
currently work with most computations.
The best option we can fit our computation into is
Aperf.array_iter_approx.
We also use [@perforatenote perforated] which
hooks into aperf and saves the used perforation to
the variable perforated.
We use this to extrapolate the final summation value.
The final, awkward code:
Aperf.array_iter_approx (fun a -> answer := !answer + a) arr [@perforatenote perforated] ;
answer := int_of_float ((float_of_int !answer) *. (1. /. !perforated)) ;
Training
We perform initial exploration using 30 input sets of 100 numbers between 0 and 100,000. Below is a graph of the accuracy loss of an exhaustive search of perforation while keeping $x$ out of the 100 numbers.
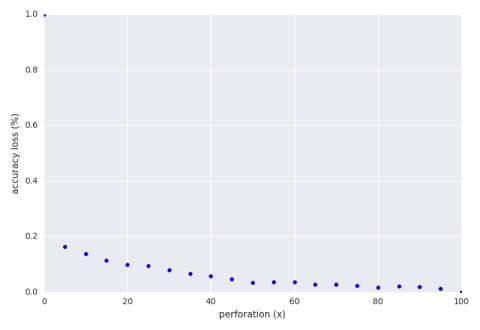
Note that we are well below the theoretical loss. Below is a graph of the accuracy loss of a hill climbing run of the perforation with an accuracy loss bound of 30%.
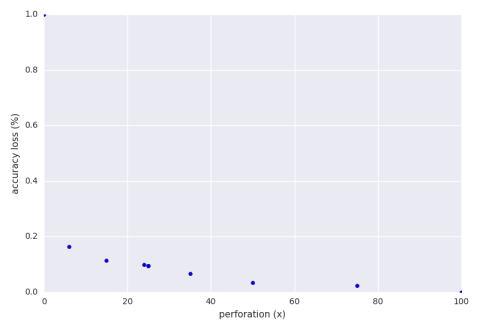
Our exploration finds that a perforation of 15% is adequate. This means that out of 100 numbers we are only summing 15 of them. From this we get a speedup of 3.6x and an accuracy loss of 11%.
It specifically chose 15% because it had a good combination of high speedup and low accuracy loss. Among the other configurations the system tried was 35%. It had a speedup of 2.3x and an accuracy loss of 9.5%. Why wasn’t it chosen? The program saw that with just a 1.5% further sacrifice of accuracy the system was able to decrease run time by over one factor. Another configuration the system tried was 6% which has an impressive speedup of 7.9x at an accuracy loss of 16%. The system, as programmed now, did not want to sacrifice an extra 5% accuracy loss for the extra speed. Perhaps if aperf supported user defined climbing strategies then someone could program a strategy which accepted that tradeoff and explored further.
If we require an accuracy loss bound of 5% then aperf finds a perforation of 50% to be the best result which gives a speedup of 1.3x and an accuracy loss of 3.5%.
Testing
We test the two perforation results from the 30% accuracy bound and the 5% accuracy bound on 10 testing sets each of 30 input sets of 100 numbers between 0 and 100,000. This is to test the generalization of the perforation—we want the perforation to work equally well on data it wasn’t trained for. Over 10 runs, with perforation 15% the average accuracy loss is 11.8% and with perforation 50% the average accuracy loss is 5.2%.
We then run the same experiment but with inputs drawn from the range $[0, 1{,}000{,}000]$. This is to test the scalability of the perforation—we want the perforation to work well for larger ranges of data than those it was trained for. Over 10 runs, with perforation 15% the average accuracy loss is 10.4% and with perforation 50% the average accuracy loss is 4.8%.
It looks like the perforation is generalizing and scaling nicely. Of course this is a simple problem and we’d like to explore some results from a more complex domain.
K-means
We perforate two loops in K-means
- the loop over the points when finding new centers
- the number of iterations of the step algorithm
Training
We initially train on 30 inputs of 1,000 2-dimensional points where values in each dimension range from 0 to 500. Below is a graph of the speedup vs. accuracy loss of an exhaustive search of perforation.
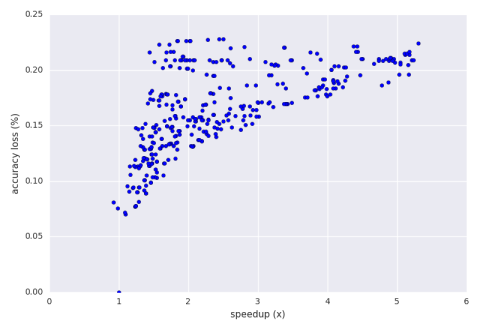
Below is a graph of the speedup vs. accuracy loss of a hill climbing run of the perforation with an accuracy loss bound of 30%.
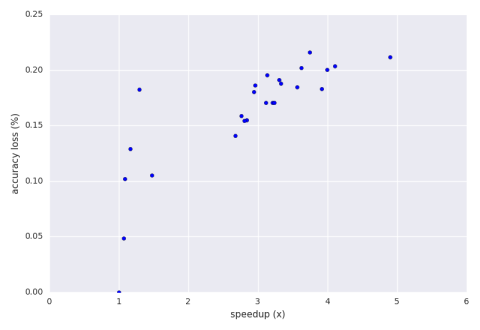
The result aperf picked in the end was 44% perforation for the points loop and 33% perforation for the step algorithm. This configuration had a speedup of 2.8x and an accuracy loss of 15.5%. If the user wishes to move upwards into the 3x speedup range then there are some results there that offer 17% accuracy loss and above as seen on the graph. Again, this is all about efficiently exploring the perforation configuration space. Different strategies could be a future feature.
Testing
We test on 30 inputs of 1,000 2-dimensional points where values in each dimension range from 0 to 1,000. This tests whether the perforation scales with larger ranges on the dimensions. Over 10 runs, the average speedup is 2.8x and the average accuracy loss is 16.8%.
We also test on 30 inputs of 10,000 2-dimensional points with the same dimension ranges. This tests if the perforation scales with the number of points in each input set. Over 10 runs, the average speedup is 3.2x and the average accuracy loss is 14.3%.
Finally, we test on 30 inputs of 10,000 2-dimensional points where values in each dimension range from 0 to 5,000. This tests if the perforation scales with larger ranges in the dimensions as well as the number of points in each input set. Over 30 runs, the average speedup is 3.2x and the average accuracy loss is 13.0%.
The perforation seems to be scaling nicely.
Further
We should test more computations with aperf. I’m excited to see how the community may use this tool and I’m willing to work with anyone who wants to use aperf.
📎 The Difficulty in a General Approximate Computing Framework
15 Jul 2016
Approximate computing is sacrificing accuracy in the hopes of reducing resource usage.
Application specific techniques in this space require too much domain specific knowledge to be used as generic solutions for approximate programming.
I will go through some common techniques in approximate computing, why they don’t work well as generic solutions, and then offer a potential future direction.
Statically Bounding Error
One commonly sought after goal in approximate computing is to statically bound the absolute error of a computation. The most applied approach for accomplishing this is to statically recognize patterns of computation and use statistical techniques to derive bounds1 2.
For example, we can use Hoeffding’s Inequality to approximate the summation of variables. Unfortunately it’s use is constrained in that the variables it sums must be independent and bounded by some interval $[a,b]$. If we meet these constraints then we can give the following error bound, with a probability of at least $1-\epsilon$, on a summation of only $m$ numbers out of an original $n$-number summation:
With further use of statistical techniques, it is possible to derive static absolute error bounds when calculating mean, argmin-sum, and ratio. However, depending on which statistical technique you use, you might have to prove or assume i.i.d.-ness of random variables, that sequences of random variables are random walks, the distribution of random variables, or other properties. These are all very domain dependent properties which don’t fit well into a generic programming framework. Further, the patterns of computation these techniques work for (i.e. sum, mean, argmin-sum, and ratio) are very low level; it’s unclear whether these techniques can scale to high-level algorithms without running into very advanced statistical techniques. For example, how would the error bounds on a sum help you give error bounds on a Fourier transform?
Reasoning and Proving
There has been at least one effort in offering programmers the chance to reason and prove properties of approximate programs3. The dream is that you would be able to prove more complex properties about more complex calculations than the pattern recognition tools offer.
For example, the referenced paper gives an example of reasoning over a program which skips locks to speed up execution time. The program is 14 lines. The reasoning, done in Coq, statically bounds the error on the calculation. The proof is 223 lines (not counting comments, blank lines, or the almost 5k lines of Coq which make up the library which powers the proof). I am not pointing out the line counts because I do not believe in this approach. On the contrary, I do believe in this approach—I just don’t think it’s feasible to expect an average programmer today to reason about their approximate programs using this framework. Maybe in a few years; not now.
A Hands on Approach
I do not believe that static analysis via pattern detection is a good fit for generic approximate computing. I do believe that proving and reasoning could become a good generic solution if and when proof automation becomes more mainstream. I believe the closest we can get today to a generic solution is to offer programmers a toolbox which allows them to explore the effects of approximate programming techniques in a hands on manner.
I’ve started writing a user-guided loop perforation system called aperf. The code is on github. Right now it only supports loop perforation. Loop perforation is when some iterations of a process are dropped in the name of approximate computing. The goal is to drop as much as possible while still maintaining an acceptable error/resource tradeoff. aperf takes an annotated source program as input and automatically searches the error/time tradeoff space for a pareto curve. A detailed report of the perforation options are returned the user.
View on GitHub